Was, werte Leser, haben eine Rose, die Kathedrale von Chartres, die griechische Akropolis, die Pyramiden aus Ägypten und die Keplersche Theorie der Sphärenharmonie sowie der erste Satz des Werkes “Musik für Saiteninstrumente, Schlagwerk und Celesta” von Bela Bartok gemeinsam?
Sie beruhen alle auf demselben Ordnungsprinzip: Dem in der Natur, der Wissenschaft, der Kunst und der Musik vorkommenden
Goldenen Schnitt,
die – wie man sie nennt –
Mathematische Sprache der Schönheit.
„In der Welt zu leben, ohne Einblick in die versteckten Gesetze der Natur ist so, als kenne man die Sprache des Landes nicht, in dem man geboren wurde.“
Haart Inayat Khan
Die Suche nach der Erkenntnis, mit dem Ziel, die uns umgebende Welt zu verstehen, bestimmt Teile unseres Lebens.
Durch wen und durch was wird unsere Existenz, unsere Gesundheit, werden unsere Überlebensmöglichkeiten geschaffen?
Wer oder was definiert unseren Begriff von Harmonie, von Schönheit, von Natur, von Kunst, von Musik?
Diese Suche nach dem Verstehen treibt viele von uns Menschen an, zu leben, morgens aufzustehen und zu schauen was es noch zu tun gibt, um hinter die Dinge zu kommen.

Die göttliche Proportion
Schon früh erkannte die Menschheit, dass es das Phänomen der Proportionen war, die Antworten gaben. Dass es hier Bereiche gibt, in denen Erkenntnis gefunden werden konnte.
Schon das morgendliche Betrachten von uns selbst im Spiegel zeigt uns dies täglich immer wieder aufs Neue. Wenn wir weiter weg vom Spiegel gehen, sehen wir mehr von uns, werden aber immer kleiner.
Gehen wir näher heran, geschieht das Gegenteil. Das bedeutet dass nah sich zu groß wie entfernt zu klein verhält.
Hiermit ist eine Proportion definiert: Die Größe der Spiegelung ist proportional zur Entfernung zum Spiegel.
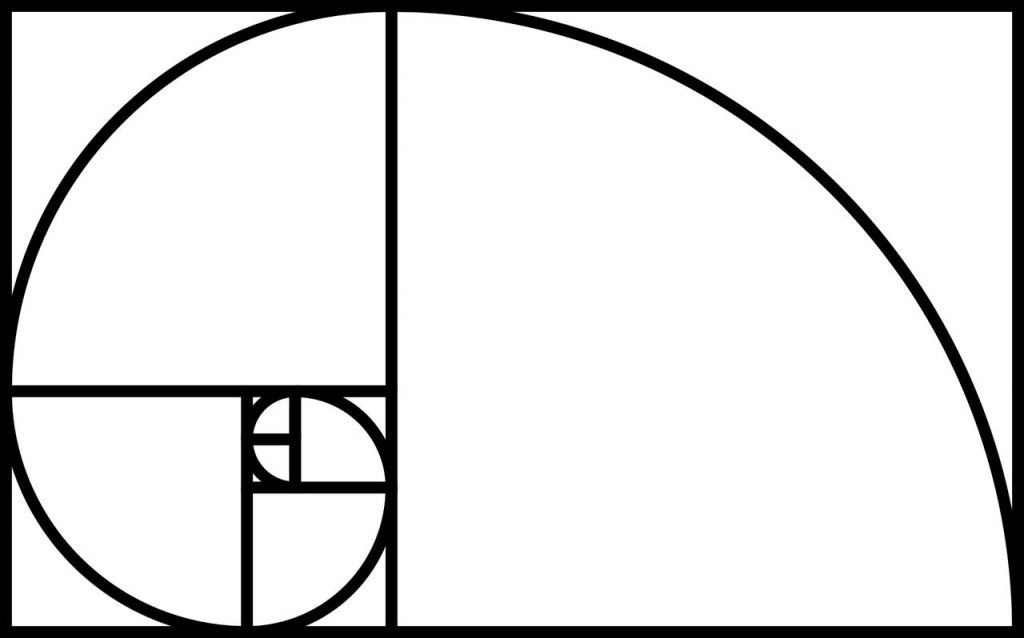
Die Forscher des Goldenen Schnitts
So in etwa müssen Sie sich die Entdeckungen vorstellen, die sich nach und nach der Erkenntnis aus dem Phänomen des Goldenen Schnitts näherten.
Und es ist mit unendlich vielen Menschen, Forschern, Mathematikern, Physikern, Naturuntersuchern, Malern, Bildhauern, Schriftstellern und natürlich Musikern verbunden, die sich diesen Gesetzmäßigkeiten zuwandten.
Phidias, geboren im 4. Jhd. v.Chr., war ein Bildhauer, der nachweislich den goldenen Schnitt schon auf seine Skulpturen anwandte.
Zu ihm hinzu kommen noch Platon und Euklid, der die Zahlen definierte. Fibonacci,der die gleichnamige Reihe erfand.
Kepler, der die Sphärenharmonie beschrieb.
Auch Bonnet, Ohm und Penrose sind an dieser Stelle zu nennen.
Über jeden hier wäre einfach unendlich viel zu sagen.
„Seit Jahrhunderten sind Menschen vom Goldenen Schnitt fasziniert. Das liegt zum Großteil an seinen bemerkenswerten Eigenschaften – Harmonie, Regeneration und Gleichgewicht sind nur einige davon. Auch die Natur bedient sich seiner Harmonie – sie erscheint in Pflanzen, Muscheln, Wind und Sternen.
Das regenerative Prinzip findet sich in Formen und Körpern, die als Basis für die DNA bis hin zu den Konturen des Universums dienen. Die Balance ist ebenso in der Spirale des Innenohres wie auch in der Form eines eingerollten menschlichen Embryos zu sehen.“

Die Fibonacci-Reihe
Ich drohe mich mal wieder in meiner eigenen Begeisterung zu verlaufen – ich könnte stundenlang weiter erzählen und mich in die Denkweisen der aufgelisteten Personen vertiefen. Schon allein die Geschichte der Zahlen ist ein unglaubliches Thema (z.B. die heiligen Sieben usw.).
Es gibt Geometrie im Summen der Saiten…
es gibt Musik in den Abständen der Sphären.
Pythagoras
Und hier sind wir mitten in der Musik.
Der Mathematiker Leonardo von Pisa, heute bekannt als Fibonacci, war mehr als ein Mathematiker. Er war ein Art Universalgelehrter, der im 13. Jhd. n. Chr. lebte und dessen Name mit der gleichnamigen Fibonacci-Reihe in Verbindung steht.

Der goldene Schnitt ist, wie am Anfang schon dargestellt, ein Proportionen-Phänomen.
Auf eine Strecke, eine Linie übertragen, gehe ich von der frei festgelegten Länge der Linie mit der Bezeichnung A aus:
A –––––––––––––––––––––––––––––––––––
Diese Linie A wird in die Teile B & C geteilt:
B ––––––––––––––––––––––– C ––––––––––
Untersucht man diese Verhältnisse, dann ergibt sich die Beziehung:
_A_ = _B_
B C
Diese Formel stellt also eine Proportion dar.
Sie können dies gerne einmal ausprobieren und mit einem Seil nachmessen oder nachzeichnen (Letzteres werde ich das nächste Mal genauer erläutern).
Die Fibonaccireihe gestaltet sich folgendermaßen: Ausgehend von 1 folgt noch einmal die Zahl 1. Als nächstes werden die beiden Zahlen zusammengezählt, womit sich die 2 ergibt.
Dann werden 2 + 1 zusammen gezählt und es ergibt sich 3. Anschließend folgt die Addition von 2 + 3 = 5 und 3 + 5 = 8. Was muss sich nun demnach als nächstes ergeben? Richtig: 5 + 8 = 13.
Daraus ergibt sich folgende Reihe: 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 …
Der Geheime Code der Musik
“Was hat das mit dem Goldenen Schnitt zu tun?”, werden Sie fragen. Ich komme zurück zur Musik, zur Ordnung der Tonhöhen, der Rythmen, der Farben und zeige anhand eines Beispiels wie ich und viele Musiker arbeiten.
Jede Musik verläuft in der Zeit – das ist logisch – und diesen Zeitablauf haben wir dergestalt zu komponieren, dass das, was wir ausdrücken wollen, auch beim Hörer ankommt.

Als erstes ist es bedeutungsvoll zu entscheiden, wie wir anfangen – der Beginn macht zwei Drittel des Erfolgs aus.
Danach haben wir den Schluss zu bedenken: Wie endet unser Stück? Auch hier muss genau nachgedacht und geplant werden!
Also haben wir einen
ANFANG ———————————————— & einen SCHLUSS————
Nun kommt die Frage auf, was dazwischen zu tun ist. Alle Stücke haben eine Struktur: Früher waren es Themen, Motive, Kontrapunkte, Durchführungen. Heute sind es Gestalten, Sounds, Patterns usw.
Die Mehrzahl aller Stücke haben zumindest einen Höhepunkt, dort wo alles groß, mächtig und laut ist. Also haben wir einen Anfang, einen Höhepunkt und einen Schluss.
Dazwischen wird langsam der Höhepunkt entwickelt, woraufhin das Stück allmählich leiser und dann eventuell auch langsamer wird.

Ich lege nun einmal fest, dass meine Komposition 89 Takte hat. Der Anfang ist der 1. Takt, der Schluss ist bei Takt 89.
Nun ist die Frage, an welcher Stelle der Höhepunkt kommt, so dass er auch seine größtmögliche Wirkung erzielt?
Anfang Takt 1 ——————————————————————————————Schluss Takt 89.
Um den größten Effekt zu erzielen, nehme ich die Fibonacci-Reihe zur Hilfe, die mir den Goldenen Schnittvermittelt:
1 2 3 5 8 13 21 34 55 89
Diese Reihe sagt mir, dass der Höhepunkt des Stückes nicht in der Mitte – bei Takt 44,5 – sein darf, sondern in Takt 55.
Der erste Teil, der Aufbau des Stückes, benötigt 55 Takte, um den Höhepunkt zu erreichen und 34 Takte, um ihn wieder abzubauen. Wenn ich das tue, dann empfinden die Zuhörer beide Teile als gleich lang.
Würde ich den Höhepunkt in der Mitte setzen, würden die Hörer den zweiten Teil als zu lang empfinden und das Stück als schlecht und nicht gelungen ablehnen.
Von der Musik bis hin zur Natur
Sie werden vielleicht denken, dass dies eine rechnerische Spielerei ist. Sie können sich selbst überzeugen, dass dem nicht so ist!
Der oben aufgezeigte Plan ist der Plan für eine reale Musik, komponiert von Bela Bartok als erster Satz in seinem Werk: “Musik für Saiteninstrumente, Schlagzeug und Celesta”.
Sie können es sich gern hier anhören. Wenn Sie Interesse an den Details haben, kann ich Ihnen auch gerne die Analyse zusenden.

Übrigens ist die Fibonacci-Reihe ebenso in der Rosenknospe zu sehen, in der Anzahl der Blütenblätter des Gänseblümchens, der Genealogie einer männlichen Bienendrohne, bei den Einzelblüten der Ananas, der Sonnenblumen und der Erdbeeren, die durch zwei Spiralsysteme radial von einem Zentrum ausgehen.
Oder schauen Sie sich einmal die Spirale eines Hurrikans an, van Goghs “Sternenlicht”… Sie werden unendlich viel Beispiele finden!
Nach diesem ersten Anfang über den Goldenen Schnitt ende ich mit einem Satz von Van der Leeuw:
Das wahre Geheimnis des Lebens ist nicht ein Problem,
das gelöst werden muss,
es ist die Wirklichkeit,
die erlebt werden sollte.
Herzlich,
Ihr Klaus Fessmann