1. Lieber Herr Warm: Ich kenne Sie und Ihre Arbeiten nun schon seit vielen Jahren, bin aber immer wieder aufs Neue von Ihrem Tun fasziniert. Würden Sie zustimmen, wenn ich Sie als Pythagoras des 21. Jahrhunderts bezeichnen würde? Wenn ja, bitte ich um Ihre Sicht der Dinge!
Wenn Sie, lieber Herr Prof. Fessmann, als Schöpfer oder zumindest Wiedererwecker und Erneuerer der KlangStein-Musik und als mehrfacher Kultur-Preisträger, mich als Pythagoras des 21. Jahrhunderts bezeichnen möchten, ist das natürlich eine große Ehre für mich und eine Bestätigung für meine Arbeiten.
Auf der anderen Seite möchte ich realistisch bleiben.
Pythagoras und auch Johannes Kepler, der zweite große Mann auf dem Gebiet der Sphärenharmonie, waren universelle Geister, die auf verschiedenen Gebieten ihr ganzes Leben lang Herausragendes geleistet haben, und auch durch ihr persönliches Leben als Vorbild angesehen werden können.
Ich habe mit etwa 40 Jahren begonnen, mich intensiv mit der Idee der Sphärenharmonie zu beschäftigen.
Ich wollte zu der Zeit, zunächst aufgrund einer vertieften Beschäftigung mit der philosophischen Bedeutung der Musik, einfach wissen, was es mit dieser Idee vor dem Hintergrund moderner astronomischer Möglichkeiten tatsächlich auf sich hat.
Ich hatte dann das Glück, einige Dinge über die Ordnung in unserem Sonnensystem entdecken zu können, welche die Grundgedanken von Pythagoras und Kepler zu diesem Thema bestätigt und – ich glaube schon, dass ich das ohne Selbstüberschätzung sagen kann – auf eine zeitgemäße Stufe gehoben haben.
Wenn Sie mich daher auf dem Gebiet der Sphärenharmonie bzw. der Welt-Harmonik, wie Kepler es nannte – aber nur auf diesem – hinter Pythagoras und Kepler als Nummer drei anführen, freue ich mich sehr und kann das akzeptieren.
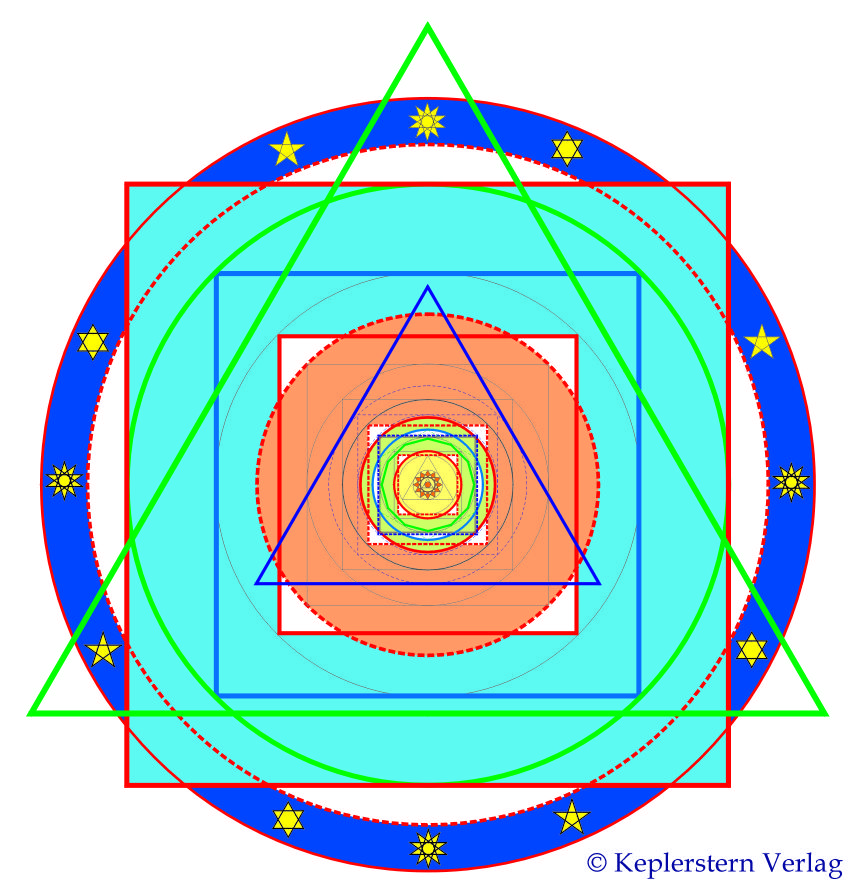
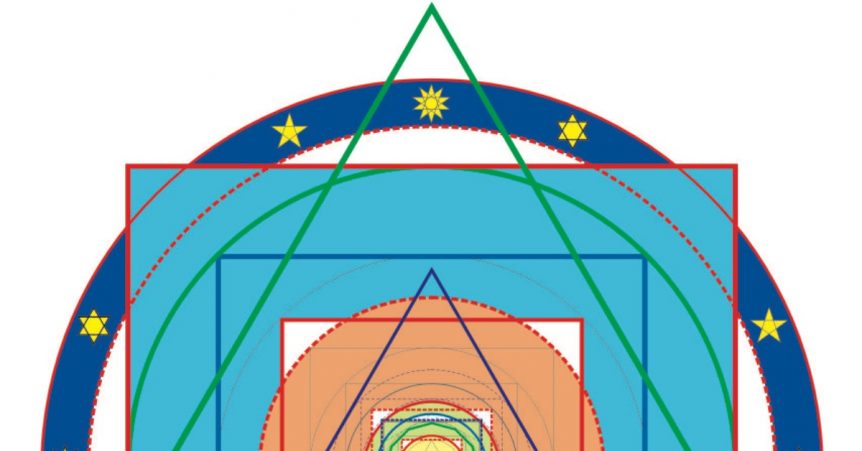
Abbildung 1: Die ursprüngliche Signatur der Sphären.
Dargestellt sind geometrische Entsprechungen für die Verhältnisse der Kleinen Halbachsen aller 9 Planeten (inkl. Pluto). Eine detaillierte Erläuterung würde den Rahmen hier sprengen und ist in Kapitel 13 des gleichnamigen Buches zu finden.
2. Musica instrumentalis, Musica humana und Musica mundana sind für mich seit langem zentrale Begriffe für meine Musik. Sind Sie hierüber auf die Signatur der Sphären gelangt?
So kann man es ausdrücken. Um es genauer zu erläutern: Die Musica mundana aus dem Konzept des Boethius (6. Jhdt. nach Chr.) entspricht ja der pythagoräischen Sphärenharmonie.
Musica instrumentalis, Musica humana und Musica mundana haben als gemeinsame Grundlage die musikalisch-harmonischen Zahlenproprotionen 2:1 (Oktave), 3:2 (Quinte), 4:3 (Quarte) etc.
Man hatte also die Vorstellung, dass auch im Kosmos (d.h. im Bereich der Sphären) diese Proportionen zu finden sind. Es gab verschiedene intuitive Zuordnungen, was das denn nun konkret bedeuten soll.
Die Abstände der Planetenbahnen, ihre Umlaufzeiten wurde unter anderem ins Spiel gebracht. Doch man hatte keine genauen Daten, um zu einem eindeutigen Resultat zu kommen.
Diese Situation änderte sich erst im 17. Jahrhundert mit Johannes Kepler, der die Planetengesetze fand und dadurch sehr viel genauere Berechnungen möglich machte. Kepler untersuchte die Verhältnisse im Sonnensystem mit seinen neuen Möglichkeiten sehr gründlich.
Er kam schließlich zu der Überzeugung, dass die Proportionen der Winkelgeschwindigkeiten (oder der von der Sonne aus gesehenen Winkeln, wie Kepler es formulierte) eine sehr gute Übereinstimmung mit den musikalischen Intervallen aufweisen.
In der Literatur konnte ich eigenartigerweise keine befriedigende Antwort darauf finden, ob das denn nun tatsächlich zutrifft. Es gab nur Stimmen, die an die Sphärenharmonie glauben und andere, die glauben, dass das nur eine Träumerei von gestern sei.
Ich fand jedoch keine ernsthafte und wirklich durchdachte wissenschaftliche Untersuchung darüber. Darum begann ich, der Sache selbst auf den Grund zu gehen.

Abbildung 2: Raumgeraden (gedachte Verbindungslinien, aufgetragen in der Ebene der Ekliptik) Venus-Erde. Alle vier Tage. Zeitraum: Acht Jahre.
3. Würden Sie bitte den Begriff der Signatur der Sphären und Ihre Vorgehensweise unseren Lesern erläutern?
Da fange ich am besten mit der Vorgehensweise an. Zunächst ging es mir um die vermeintlichen Übereinstimmungen zwischen planetarischen und musikalischen Verhältnissen.
Kepler behauptete nicht, dass diese 100-%ig, sondern dass sie sehr genau sind. Was heißt hier aber genau?
Vor allem, wenn wir zum Beispiel zwölf Intervalle haben (damals waren sechs Planeten bekannt, jeder hat bei Kepler zwei Werte), die alle ein wenig von den idealen Proportionen abweichen. Ist das dann noch insgesamt gut?
Um es kurz zu sagen: Diese Frage lässt sich nur mit Methoden der Wahrscheinlichkeitsrechnung klären (welche es zu Keplers Zeit noch nicht gab). Dies habe ich also zuerst getan.
Ich fand schließlich Parameter (andere als die von Kepler gedachten), in deren Intervallen in der Tat eine statistisch hochsignifikante Übereinstimmung mit musikalischen Intervallen vorliegt.
Danach habe ich die räumlichen Abstände der Planetenbahnen untersucht. Kepler hatte hierzu ein Modell mit den ineinander geschachtelten platonischen Körpern entwickelt, wobei ihm aber nach einiger Zeit klar wurde, daß dieses nur sehr grob zutrifft.
Ich fand klare geometrische Zusammenhänge der Bahnen, die sich aus Kombinationen der einfachsten Figuren – Kreis, Quadrat und Dreieck – ergeben. Quadrat und Dreieck kann man im Zwölfstern vereinigen.
Ein Gesamtbild aus diesen Figuren, in das alle Planeten einbezogen sind, nannte ich zunächst “Die Signatur der Sphären” (siehe Abbildung 1).
Weiterhin untersuchte ich die Bewegungen, wobei es mir vor allem auf die langfristigen Beziehungen zwischen den Planeten ankam.
Hier entdeckte ich die planetarischen Bewegungsfiguren, wie beispielhaft in den Abbildungen zwei bis vier zu sehen ist.
Im Laufe der Zeit wurden für mich eher diese Bilder zu den Signaturen. Eine Signatur ist eine Art Unterschrift. In diesem Sinne drückt sich für mich in all dem, was ich entdecken konnte, etwas Geistiges aus.

Abbildung 3: Mars aus Venus-Sicht bei Venus/Neptun-Konjunktionen. Zeitraum: 357 Jahre. Die Punkte geben die Mars-Positionen an, die Linien die chronologischen Verbindungslinien.
4. Wie würden Sie die Ordnungen und Schönheiten des Kosmos beschreiben und welche Bedeutung haben diese für Sie?
Dies muss man im Zusammenhang mit dem Bild vom Kosmos sehen, das uns die heutige Astronomie präsentiert.
Zwar gibt es unermesslich schöne Aufnahmen von Spiralgalaxien und planetarischen Nebeln etc., insgesamt wird aber eine Anschauung vertreten, die für die Idee einer Sphärenharmonie wenig Raum lässt.
Urknall, Schwarze Löcher, Super-Nova-Explosionen, Gammastrahlenblitze und derartige Phänomene können dem Menschen wohl kaum einen geistigen Halt geben, insbesondere, wenn man glaubt, dass alles allein durch eine Kombination von Zufall und Naturgesetzen entstanden ist – inklusive unserer Lebensspenderin, der Sonne, und der Erde, auf der wir unsere Existenz haben.
Doch was wissen wir wirklich?
Es ist zum Beispiel noch nicht einmal geklärt, worauf die langfristige Stabilität des Sonnensystems eigentlich beruht. Diese könnte durchaus mit der auf fast unglaubliche Weise vielschichtig nach der Zahl 12 geordneten Beziehung der massereichsten Planeten Jupiter, Saturn und Neptun zusammenhängen, die für diese Stabilität die größte Rolle spielen (Beispiel siehe Abbildung 4).
Dass es also zumindest in unserem kosmischen Nahbereich, dem Sonnensystem, eine grandiose und oftmals sehr ästhetische geometrische Ordnung gibt, und auch die früheren Vorstellungen einer Übereinstimmung mit musikalischen Intervallen sich bestätigt haben, hat nach meiner Einschätzung eine große Bedeutung für unser modernes Weltbild (oder vielleicht eher für das “postmoderne”).
Auch wenn sich hier, wie es scheint, etwas Geheimnisvolles, Schöpferisches offenbart, das uns unmittelbar und tief berühren kann, gibt es keine einfache Antwort, woher diese Ordnung kommt und was sie sagen will.
Es ist eher mit einer Musik zu vergleichen. Auch hier muss jeder in sich selbst hineinhorchen, ob diese Musik eine Bedeutung für ihn hat.
Wenn ein anderer sagt, eine Musik ist schön oder erhaben, und ich empfinde das nicht so, nützt mir das wenig.

Abbildung 4: Raumgeraden Jupiter-Neptun bei Jupiter/Saturn-Konjunktionen. Zeitraum: 14894 Jahre.
5. Seit ich angefangen habe mit den KlangSteinen zu musizieren, denke ich daran, dass in dieser Art und Weise die Sphären-Harmonie-Musik klingt. Das Quadrivium Arithmetik, Geometrie, Musik und Astronomie gibt hier den Weg vor. Und dadurch folge ich Ihren Signaturen beim Komponieren.
Was halten Sie davon?
Was Menschen unter Sphärenharmonie verstehen, weist ein sehr breites Spektrum auf. Zum einen geht es um etwas tatsächlich oder in der Vorstellung Erklingendes.
Pythagoras konnte sie der Legende nach erlauschen. Rudolf Steiner sagt, dass die Sphärenharmonie in der geistigen Welt ertönt. Verschiedene Berichte von anderen sind in der Literatur zu finden, die sie gehört haben wollen, u.a. bei Nahtoderlebnissen.
Ich habe im vierten Kapitel meines Buches “Die Signatur der Sphären” eine Reihe solcher Äußerungen eingebaut.
Es wird dabei deutlich, dass das Erleben dieser Klänge zum einen ein individuelles ist, zum anderen an die Zeit und ihr musikalisches Schaffen gebunden ist, aus der die Äußerung stammt.
Zum zweiten wird in der Nachfolge von Pythagoras und Kepler von Sphärenharmonie gesprochen, wenn es um eine arithmetische Übereinstimmung von Intervallen gibt, die sich in Geometrie, Musik, Astronomie und auch noch anderem kundtun kann.
Auch meine Arbeiten betreffen vor allem diesen zweiten Aspekt. Das, was die beiden Bereiche miteinander verbindet, sind nach Johannes Kepler die Archetypen.
Darunter verstand er geistige Urbilder der Schöpfung, die im Äußeren (in der Welt) und auch im menschlichen Inneren (in der Seele) zu finden sind.
So kann man sagen, dass sowohl die Musik der Steine als auch die Signaturen der Planetenbeziehungen auf diesen Archetypen gründen. Und wenn ich Ihre Musik höre, bin ich vermutlich nicht der Einzige, für den sie oftmals etwas Sphärisches hat.
Herzlich
Ihr Klaus Fessmann